watches the people with basic math skills fight to the death over the answer
If you really wanna see a bloodbath, watch this:
You know that a couple has two children. You go to the couple’s house and one of their children, a young boy, opens the door. What is the probability that the couple’s other child is a girl?
50%, since the coins are independent, right?
Oops, I changed it to a more unintuitive one right after you replied! In my original comment, I said “you flip two coins, and you only know that at least one of them landed on heads. What is the probability that both landed on heads?”
And… No! Conditional probability strikes again! When you flipped those coins, the four possible outcomes were TT, TH, HT, HH
When you found out that at least one coin landed on heads, all you did was rule out TT. Now the possibilities are HT, TH, and HH. There’s actually only a 1/3 chance that both are heads! If I had specified that one particular coin landed on heads, then it would be 50%
No. It’s still 50-50. Observing doesn’t change probabilities (except maybe in quantum lol). This isn’t like the Monty Hall where you make a choice.
The problem is that you stopped your probably tree too early. There is the chance that the first kid is a boy, the chance the second kid is a boy, AND the chance that the first kid answered the door. Here is the full tree, the gender of the first kid, the gender of the second and which child opened the door, last we see if your observation (boy at the door) excludes that scenario.
1 2 D E
B B 1 N
B G 1 N
G B 1 Y
G G 1 Y
B B 2 N
B G 2 Y
G B 2 N
G G 2 Y
You can see that of the scenarios that are not excluded there are two where the other child is a boy and two there the other child is a girl. 50-50. Observing doesn’t affect probabilities of events because your have to include the odds that you observe what you observed.
I was about to reply to you with a comment that started with “oh shit you’re right!” But as I wrote it I started rethinking and I’m not sure now.
Because I actually don’t think it matters whether we’re BB1 or BB2. They’re both only one generation of the four possible initial states. Which child opens the door is determined after the determination of which child is which gender. Basically, given that they have two boys, we’re guaranteed to see a boy, so you shouldn’t count it twice.
Still, I’m now no where near as confident in my answer as I was a moment ago. I might actually go and write the code to perform the experiment as I outlined in an earlier comment (let me know if you think that methodology is flawed/biased, and how you think it should be changed) to see what happens.
That’s a great idea let me know how it turns out. If you randomly pick the genders and randomly pick who opens the door, I think it will be 50-50. With these kinds of things they can get pretty tricky. Just because an explanation seems to make sense doesn’t mean it’s right so I’m curious!
I put it together. Here’s the code I wrote in Python.
import random genders = ['boy', 'girl'] def run(): other_child_girls = 0 for i in range(10000): other_child = get_other_child() if other_child == 'girl': other_child_girls += 1 print(other_child_girls) def get_other_child(): children = random.choices(genders, k=2) first_child_index = random.randint(0, 1) first_child = children[first_child_index] if first_child == 'boy': other_child_index = (first_child_index + 1) % 2 return children[other_child_index] # Recursively repeat this call until the child at the door is a boy # (i.e., discard any cases where the child at the door is a girl) return get_other_child() if __name__ == '__main__': run()And it turns out you were right. I ran it a few times and got answers ranging from 4942 to 5087, i.e., clustered around 50%.
And this interaction is why lemmy (and others) is superior. No “fuck you, you’re wrong” just “well I think it’s this” followed by “okay, let me try that” 10/10
Yes! They responded to my comment before the edit, where I gave the coin example: “I flipped two coins, at least one of them was heads. What is the probability that both of them are heads?”
Before I read their reply, I edited it to the more confusing and infuriating two kids example. It’s annoying because it seems like it should be the same as saying “I have two children, and at least one is a boy. What is the probability that I have two boys?” In both the coin case and this one, the answer is 1/3, but when one child answers the door, it’s like sliding one quarter out from behind my hand. Now you know a particular (child, coin)'s (sex, face), and the answer is 50% again.
deleted by creator
You assume that the probability of TH = HT = HH
When In fact, the probabilities are as follows:
P(HT)+P(TH) = 50% P(HH) = 50%
For all the probabilities being equal, you’d have to consider 4 cases:
HT, TH, HH (1) and HH (2).
The difference between HH (1) and HH (2) is which one you were told that was heads.
Then P(HH) = P(HH (1)) + P(HH (2)) = 2/4 = 50%
The issue is that you weren’t told a particular one was heads, only that at least one was heads. If I flipped a nickel and a dime, then the four possibilities are NtDt, NtDh, NhDt, and NhDh. If I say that at least one of them is heads but don’t tell you which one, then there are three possibilities: I flipped NhDt, NtDh, or NhDh. It’s only when I tell you that the nickel landed on heads that it collapses to NhDt and NhDh.
Sorry if the acronyms are hard to read, they’re much faster than typing something like “Heads (nickel) tails (dime)”
deleted by creator
Again, you are assuming that every occurrence has the same chance. When in fact, they have not. There are 3 random events happening here:
- Flip of one coin (50% chance each)
- Flip of the other coin (50% chance each)
- The coin that you told me (let’s say it’s 50% nickel 50% dime for simplicity’s sake)
Also, I am assuming that these 3 events are completely unrelated. That is, the result of a coin flip won’t determine whether you tell me the nickel or dime. A complete list of events is as follows:
T T N
T T D
H T N
H T D
T H N
T H D
H H N
H H D
After telling me that one of them is heads, the list is as follows:
H T D
T H N
H H D
H H N
H H is 50% chance, and the sum of HT + TH is the other 50%
This is very easily simulated. I use Tasker, you can use Python or something. Assume 1 is heads and 2 is tails
-
Randomize variable %dime to 1 or 2
-
Randomize variable %nickel to 1 or 2
This flips two coins. At this point there’s a 25% chance of each TT, TH, HT, and HH occurring.
- Goto 1 IF %dime != 1 AND %nickel != 1
This is the point where I tell you that at least one of them is heads, but not which. It flips the coins again only if they landed TT, which means there are three possible sets of coins now: TH, HT, or HH.
-
Add 1 to variable %HeadsTails IF %dime = 2 OR %nickel = 2
-
Add 1 to variable %HeadsHeads IF %dime = 1 AND %nickel = 1
This keeps track of what sets made it past line 3. If either is tails, it adds one to %HeadsTails. If neither is tails, then it adds one to %HeadsHeads
-
Add 1 to variable %Counter
-
Goto 1 IF %Counter <1000
You can set your counter as high as you like. Python would probably handle 10,000 flips faster than Tasker can handle 1,000, but I’m on my phone and also python illiterate.
Press play, and I get 357 sets with two heads, and 643 sets that have a tails. The longer it runs, the closer to a ratio of 1:2 it’ll get.
-
You’ve also ruled out TH by knowing one is heads. So the only possibilities are HT and HH. Is that not 50/50?
it depends on how you know this information. did you look at one of the coins? then it’s 50/50. did you ask a friend to look and yell you whether at least one of them is heads? then it’s 2/3.
At least one is heads, but unless you know which one it is, you haven’t ruled out HT or TH
But you do know which one it is, because you said “other child”. As soon as you ask the question, you assign a specific outcome to a specific child eliminating HH and HT (or in the new example, BB and BG). “What are the odds they have a female child” and “what are the odds the other child is female” are not the same question.
This is basically Monty Hall right? The other child is a girl with 2/3 probability, because the first one being a boy eliminates the case where both children are girls, leaving three total cases, in two of which the other child is a girl (BG, GB, BB).
Actually, it’s a Monty Hall problem because a door is opened.
Unironically, yes. A door is opened, and the opening of that door reveals information about the problem and eliminates some possible world-states.
It doesn’t, though. The Monty Hall problem utilizes the fact that there were more possibilities before one was eliminated AND that it cannot eliminate the “best” outcome. No such qualities are at play here.
The question being asked here is “what is the gender of the second child?” The gender of the first child is completely irrelevent. Observed or unobserved, door open or closed, it doesn’t impact the outcome of the second child.
I suspect it’s not the question OP intended to ask, but it’s the question they asked nonetheless.
The Monty Hall problem utilizes the fact that there were more possibilities before one was eliminated
So does this problem. There was the GG possibility.
AND that it cannot eliminate the “best” outcome.
True, this problem doesn’t have that element.
The question being asked here is “what is the gender of the second child?” The gender of the first child is completely irrelevent. Observed or unobserved, door open or closed, it doesn’t impact the outcome of the second child.
I don’t agree. First, I’d say your use of the term “second child” is ambiguous, because normally that would mean “the younger of two children”, which obviously isn’t what’s meant here. What you mean to say here is “the child that we have not already seen”. It’s in that rephrasing that it becomes obvious that having observed the first child matters, because there cannot be a second until there has been a first. And it’s in that observation that the outcome is altered.
If we haven’t seen the first child and are asked “what will be the gender of the second child to walk through the door?” we would have to answer 50/50. But having seen one child, we eliminate one of four possibilities of gender pairs (BB, BG, GB, GG). This we are left with 3 equally possible cases, 2 of which will be the opposite of the gender of the child we saw first.
Of course, we could easily simulate this experiment to arrive at an empirical answer. Randomly generate 2 genders, randomly select one of those. If they’re a girl, end the experiment and move to another iteration (because they didn’t fit the parameters). If a boy, record the gender of the other child. Repeat a few dozen times and see how many times the second child was a girl.
Well, I guess OPs point is demonstrated. People will in fact argue about it.
What you’re trying to present has multiple holes, but only one matters: you’re not paying attention to the question that’s being asked. You can say first, second, alpha, beta, Leslie, whatever you want to assign the child in question as, but the question only asks you the gender of a singular child. The door opening child doesn’t matter, because it isn’t part of the question. No one asked what gender that child is. No one asked what the odds they have a female child is. It just isn’t a part of the question.
Yes, I referred to it as the second child because the question that was asked happens to have a child in it and ask you about another. Because we’re communicating in a hilariously precise language, we have to say “the other child”. But that doesn’t make the door opening child a part of the equation. The question could be “there is a child in a box. What are the odds the child is female? Oh, it has a brother by the way.” Cool, who cares, the sibling wasn’t a part of the question.
The Monty Hall problem spreads multiple outcomes across multiple choices and then eliminates one. The outcomes and options have a relation. This question just asks you about a singular variable with two possible outcomes and throws around an unrelated red herring.
You can’t just end the experiment if the randomly chosen child doesn’t “fit the parameters”, by doing that you aren’t accounting for half the girls in the whole event pool. Half of the girls have siblings that are girls.
Being 2 girls was a possible event at the start, you can’t just remove it. This time it happened to be a boy who opened the door, but it could’ve been as likely for a girl to open it.
If it was phrased like “there are 2 siblings, only boys can open doors. Of all the houses that opened their doors, how many have a girl in them?”, then it will be 2/3. In this example, there is an initial pool of events, then I narrowed down to a smaller one (with less probability). If you “just” eliminate the GG scenario, then the set of events got smaller without reducing the set’s probability.
It’s somewhat ambiguous!
On the one hand, you might be right. This could be akin to flipping two coins and saying that at least one is heads. You’ve only eliminated GG, so BG, GB, and BB are all possible, so there’s only a 1/3 chance that both children are boys.
On the other hand, you could say this is akin to flipping two coins and saying that the one on the left (or the one who opened the door) is heads. In that case, you haven’t just ruled out GG, you’ve ruled out GB. Conditional probability is witchcraft
I don’t think the problem is conditional probability, it’s translating word problems to maths problems.
If you make the assumptions I made, the maths is unambiguous. Namely, I assumed that a child has a 50/50 probability of being born a boy or a girl. I assumed the child who opens the door is random. I don’t think I made any other assumptions that could have been made any other way. With those assumptions, I’m pretty confident my answer is the only correct one, though I’d love to see an argument otherwise.
If the probability of a child being a girl is different, say, 52%, that will affect the result.
More interestingly, if the probability of which child opens the door is different, that will affect the result. If there’s a 100% chance the elder child opens the door, it goes to 50/50 of the gender of the second child. This makes it like the “coin on the left” example you gave.
If we said the elder child is going to open the door 75% of the time…well, the maths becomes more complicated than I can be bothered with right now. But it’s an interesting scenario!
Assuming the chance of either sex is equal, this problem can be broken down into multiple cases. The first is that there are two unseen kids in the house. What’s the probability they are both boys? 1/4. Now the door opens and you see two boys. The probability both are boys is 1/1. But if you only see one boy, the problem simplifies into the probability of a child being a boy. One of the probabilistic events postulated in the original problem is fixed at 1. So the answer is 1/2.
Think of it as the two coin flip, except one coin has two heads. That simplifies to a one coin flip.
No, because knowing the first child is a boy doesn’t tell you any information about the second child.
Three doors, Girl Girl Boy
You select a door and Monty opens a door to show a Girl. You had higher odds of picking a girl door to start (2/3). So switching gives you better odds at changing to the door with the Boy because you probably picked a Girl door.
Here the child being a boy doesn’t matter and the other child can be either.
It’s 50/50 assuming genders are 50/50.
Well not really, right? BG and GB are the same scenario here, so it’s a 50/50 chance.
Even if, say, the eldest child always opened the door, it’d still be a 50/50 chance, as the eldest child being a boy eliminates the possibility of GB, leaving either BG or BB.
Ironically you’ve got the right answer, but (as you can see in some of the other conversation here) not necessarily for the right reason. It’s not necessarily that BG and GB are the same, but that BB and BB are two different scenarios worthy of being counted separately.
Why is it that BB and BB are being counted separately? I thought that order didn’t matter: you could have two girls, a boy and a girl (or vice versa, same thing), or a two boys. (And then by eliminating two girls you’d have a 50/50 chance).
Because describing it as I did in that comment is a (very) shorthand way of getting at how it was explained in full by @Hacksaw@lemmy.ca in this comment.
Just read it: makes sense now. Thanks!
That is an excellent, succinct explanation
It’s also wrong, I have since learnt. See the conversation below for why.
Cheeky bastard.
It is 50-50, though. The remaining possible states are BG and BB. Both are equally likely. Any further inference is narrative… not statistics.
The classic example of this is flipping 100 coins. If you get heads 99 times in a row… the last coin is still 50-50. Yes, it is obscenely unlikely to get heads 100 times in a row. But it’s already obscenely unlikely to get heads 99 times in a row. And it is obscenely unlikely to alternate perfectly between heads and tails. And it is obscenely unlikely to get a binary pattern spelling out the alphabet. And it is obscenely unlikely to get… literally any pattern.
Every pattern is equally unlikely, with a fair coin. We see 99 heads in a row versus 1 tails at the end, and think it narrowly averted the least-probable outcome. But only because we lump together all sequences with exactly one tails. That’s one hundred different patterns. 1-99 is not the same as 99-1. We just treat them the same because we fixate on uniformity.
Compare a non-binary choice: a ten-sided die. Thirty 1s in a row is about as unlikely as 100 heads in a row. But 1 1 1… 2 is the same as 1 1 1… 3. Getting the first 29 is pretty damn unlikely. One chance in a hundred million trillion. But the final die can land on any number 1-10. Nine of them upset the pattern our ape brains want. Wanting it doesn’t make it any more likely. Or any less likely.
It would be identically unlikely for a 10-sided die to count from 1 to 10, three times in a row. All the faces appear equally. But swap any two events and suddenly it doesn’t count. No pun intended.
If this couple had eight children, for some god-forsaken reason, and you saw seven boys, the eighth kid being another boy is not less likely for it. The possibility space has already been reduced to two possibilities out of… well nine, I suppose, if order doesn’t matter. They could have 0-8 boys. They have at least 7. The only field that says the last kid’s not a coin toss is genetics, and they say this guy’s chromosome game is strong.
You’re right, but it’s not a subversion of the Gambler’s Fallacy, it’s a subversion of conditional probability. A classic example is that I have two kids, and at least one of them is a boy. What is the probability that I have two boys?
The intuitive answer is 50%, because one kid’s sex doesn’t affect the other. But when I told you that I have two kids, there were four possibilities: GG, GB, BG, or BB. When I told you that at least one of them is a boy, all I did was take away the GG option. That means there’s only a 1 in 3 chance that I have two boys.
But by having one child answer the door, I change it yet again–now we know the sex of a particular child. We know that the child who opened the door is a boy. This is now akin to saying “I have two children, and the eldest is a boy. What is the possibility that I have two boys?” It’s a sneaky nerd snipe, because it targets specifically people who know enough about statistics to know what conditional probability is. It’s also a dangerous nerd snipe, because it’s entirely possible that my reasoning is wrong!
i hate it when ppl do nb erasure for their stupid math text problems. use anything else pls
What’s the probability of the other kid being non-binary?
And don’t forget that there’s always a slim chance that no matter the gender, the other child is GOAT.
Two more for funsies! I flipped two coins. At least one of them landed on heads. What is the probability that both landed on heads? (Note: this is what my comment originally said before I edited it)
I have two children. At least one of them is a boy born on a Tuesday. What is the probability that I have two boys?
deleted by creator
Different compilers have robbed me of all trust in order-of-operations. If there’s any possibility of ambiguity - it’s going in parentheses. If something’s fucky and I can’t tell where, well, better parenthesize my equations, just in case.
There’s quite a few calculators that get this wrong. In college, I found out that Casio calculators do things the right way, are affordable, and readily available. I stuck with it through the rest of my classes.
Casio does a wonderful job, and it’s a shame they aren’t more standard in American schooling. Texas Instruments costs more of the same jobs, and is mandatory for certain systems or tests. You need to pay like $40 for a calculator that hasn’t changed much if at all from the 1990’s.
Meanwhile I have a Casio fx-115ES Plus and it does everything that one did, plus some nice quality of life features, for less money.
$40??!! My ti that was required was like over $200!!
TI did the same thing Quark and Adobe did later on – got dominance in their markets, killed off their competition, and then sat back and rested on their laurels thinking they were untouchable
EDIT: although in part, we should thank TI for one thing – if they hadn’t monopolized the calculator market, Commodore would’ve gone into calculators instead of computers
https://en.wikipedia.org/wiki/TI-99/4A
It was a huge failure, but they tried.
Huge failure my ass. Come at me on munch man, Alpiner, or Tombstone City. Or coding vaguely racist things like Mr. Bojangles, one of the first codes in the early books.
Had one at home and used the hell out of it, don’t get me wrong. Was my first computer. Played the Zork series on that thing. But, it had issues and wasn’t a financial success.
It had fewer issues than almost anything I’ve owned since. I bet it would still work if I got the right adaptors. Wasn’t a huge financial success though. They seemed content with early coding and games, and didn’t move into word processing etc.
If you’re lucky, you can find these TI calculators in thrift shops or other similar places. I’ve been lucky since I got both of my last 2 graphing calculators at a yard sale and thrift shop respectively, for maybe around $40-$50 for both.
The TI equivalent to the Casio fx-115ES Plus is the TI-36X Pro, and they both cost $20 at Walmart.
My Casio calculators get this wrong, even the newer ones. BTW the correct answer is 16, right?
- 16 is the right answer if you use PEMDAS only:
(8 ÷ 2) × (2 + 2) - 1 is the right answer if you use implicit/explicit with PEMDAS:
8 ÷ (2 × (2 + 2)) - both are correct answers (as in if you don’t put in extra parentheses to reduce ambiguity, you should expect expect either answer)
- this is also one of the reasons why postfix and prefix notations have an advantage over infix notation
- postfix (HP, RPN, Forth):
2 2 + 8 2 ÷ × . - prefix (Lisp):
(× (÷ 8 2) (+ 2 2))
- postfix (HP, RPN, Forth):
prefix notation doesn’t need parentheses either though, at least in this case. lisp uses them for readability and to get multiple arity operators. infix doesn’t have any ambiguity either if you parenthesize all operations like that.
infix doesn’t have any ambiguity either if you parenthesize all operations like that
There isn’t any ambiguity even if you don’t.
deleted by creator
PEMDAS is actually (PE)(MD)(AS). Those that are grouped together have equal precedence and are evaluated left to right.
8 / 2 * (2+2)
8 / 2 * 4
4 * 4
16
Edit to fix formatting, maybe?
8 / 2 * (2+2)
When you added the multiply you changed the answer, because the (2+2) is now in the numerator instead of in the denominator.
16 is the right answer if you use PEMDAS only: (8 ÷ 2) × (2 + 2)
You added brackets and changed the answer. 2(2+2) is a single term, and if you break it up then you change the answer (because now the (2+2) is in the numerator instead of in the denominator).
1 is the right answer
The only right answer
both are correct answers
Nope, 1 is the only correct answer.
this is also one of the reasons why postfix and prefix notations have an advantage over infix notation
Except they don’t. This isn’t a notation problem, it’s a people don’t remember the rules of Maths problem.
- 16 is the right answer if you use PEMDAS only:
Yes
8 / 2 (2+2)
8 / 2 (4)
4 (4)
16
No 8 / 2 (2+2) 8 / 2 (4) 8 / 8 1
No. Order of operations is left to right, not right to left. 1 is wrong.
Pemdas.
Multiplication comes before division.
1 is the correct answer.
That’s wrong. Multiplication and division have equal precedence, same as addition and subtraction. You do them left to right. PEMDAS could be rewritten like PE(MD)(AS). After parentheses and exponents, it"s Multiplication and division together, then addition and subtraction together. They also teach BODMAS some places, which is “brackets, order, division and multiplication, addition and subtraction” Despite reversing the division and multiplication, it doesn’t change the order of operations. They have the same priority, so they are just done left to right. PEMDAS and BODMAS are the different shorthand for the same order of operations.
They were right but for the wrong reason. Implied multiplication–that is, a(b) or ab–often comes before explicit multiplication and division. Apparently it’s up to the person writing the equation, so the meme is intentionally and explicitly ambiguous
There’s an argument to be made that implicit multiplication comes before division, resulting in the answer 1, but all multiplication? That’s wrong, full-stop. You calculate (explicit) multiplication and division in one step, left to right. Reason being that division is technically just multiplying by the reciprocal.
deleted by creator
a(b) is a×b. Step 2 could be rewritten as 8 / 2 × 4. Working left to right, step 3 becomes 4 × 4.
No, because implicit multiplication binds more tightly than explicit. a/b© becomes a/(bש)
That’s exactly where the calculators in the op differ. For more examples, Casio calculators do implicit multiplication first, while ti’s treat it the same as explicit multiplication and division. I think that the latter is more predictable personally, but really you just need to know your calculator.
Says who?
Most maths textbooks written by mathematicians.
I don’t mean when they’re explaining “here’s how the order of operations works”. I mean in the basic way that they write more advanced problems and the answers they give for them.
This video, and the prequel to it linked in the description, go into some detail showing who uses what convention and why.
deleted by creator
deleted by creator
Yes
No.
8 / 2 (4) 8/(2x4) 8/8 1
No, 8 / 2 happens before 2 * 4.
No, 8 / 2 happens before 2 * 4
That’s (2x4). Doing division before brackets goes against the order of operations rules.
Division and multiplication are equal in the order of operations
Division and multiplication are equal in the order of operations
I didn’t say they weren’t. I said…
Doing division before brackets goes against the order of operations rules
You did 8/2x4, which is the same as (8/2)(2+2), which isn’t the same as 8/2(2+2)=8/2(4)=8/(2x4).
Depends on the system you use. Most common system worldwide and in the academic circles (the oldest of the two) has 1 as the answer.
deleted by creator
the correct answer is 16, right?
Sharp as well.
Ditto for Sharp. It’s really only Texas Instruments that is the ongoing exception to the rule.
In some countries we’re taught to treat implicit multiplications as a block, as if it was surrounded by parenthesis. Not sure what exactly this convention is called, but afaic this shit was never ambiguous here. It is a convention thing, there is no right or wrong as the convention needs to be given first. It is like arguing the spelling of color vs colour.
This is exactly right. It’s not a law of maths in the way that 1+1=2 is a law. It’s a convention of notation.
The vast majority of the time, mathematicians use implicit multiplication (aka multiplication indicated by juxtaposition) at a higher priority than division. This makes sense when you consider something like 1/2x. It’s an extremely common thing to want to write, and it would be a pain in the arse to have to write brackets there every single time. So 1/2x is universally interpreted as 1/(2x), and not (1/2)x, which would be x/2.
The same logic is what’s used here when people arrive at an answer of 1.
If you were to survey a bunch of mathematicians—and I mean people doing academic research in maths, not primary school teachers—you would find the vast majority of them would get to 1. However, you would first have to give a way to do that survey such that they don’t realise the reason they’re being surveyed, because if they realise it’s over a question like this they’ll probably end up saying “it’s deliberately ambiguous in an attempt to start arguments”.
The real answer is that anyone who deals with math a lot would never write it this way, but use fractions instead
So are you suggesting that Richard Feynman didn’t “deal with maths a lot”, then? Because there definitely exist examples where he worked within the limitations of the medium he was writing in (namely: writing in places where using bar fractions was not an option) and used juxtaposition for multiplication bound more tightly than division.

Here’s another example, from an advanced mathematics textbook:

Both show the use of juxtaposition taking precedence over division.
I should note that these screenshots are both taken from this video where you can see them with greater context and discussion on the subject.
Mind you, Feynmann clearly states this is a fraction, and denotes it with “/” likely to make sure you treat it as a fraction.
Yep with pen and paper you always write fractions as actual fractions to not confuse yourself, never a division in sight, while with papers you have a page limit to observe. Length of the bars disambiguates precedence which is important because division is not associative; a/(b/c) /= (a/b)/c. “calculate from left to right” type of rules are awkward because they prevent you from arranging stuff freely for readability. None of what he writes there has more than one division in it, chances are that if you see two divisions anywhere in his work he’s using fractional notation.
Multiplication by juxtaposition not binding tightest is something I have only ever heard from Americans citing strange abbreviations as if they were mathematical laws. We were never taught any such procedural stuff in school: If you understand the underlying laws you know what you can do with an expression and what not, it’s the difference between teaching calculation and teaching algebra.
never a division in sight
There is, especially if you’re dividing by a fraction! Division and fractions aren’t the same thing.
if you see two divisions anywhere in his work he’s using fractional notation
Not if it actually is a division and not a fraction. There’s no problem with having multiple divisions in a single expression.
Division and fractions aren’t the same thing.
Semantically, yes they are. Syntactically they’re different.
The real answer is that anyone who deals with math a lot would never write it this way
Yes, they would - it’s the standard way to write a factorised term.
but use fractions instead
Fractions and division aren’t the same thing.
Fractions and division aren’t the same thing.
Are you for real? A fraction is a shorthand for division with stronger (and therefore less ambiguous) order of operations
Are you for real?
Yes, I’m a Maths teacher.
A fraction is a shorthand for division with stronger (and therefore less ambiguous) order of operations
I added emphasis to where you nearly had it.
½ is a single term. 1÷2 is 2 terms. Terms are separated by operators (division in this case) and joined by grouping symbols (fraction bars, brackets).
1÷½=2
1÷1÷2=½ (must be done left to right)
Thus 1÷2 and ½ aren’t the same thing (they are equal in simple cases, but not the same thing), but ½ and (1÷2) are the same thing.
So 1/2x is universally interpreted as 1/(2x), and not (1/2)x, which would be x/2.
Sorry but both my phone calculator and TI-84 calculate 1/2X to be the same thing as X/2. It’s simply evaluating the equation left to right since multiplication and division have equal priorities.
X = 5
Y = 1/2X => (1/2) * X => X/2
Y = 2.5
If you want to see Y = 0.1 you must explicitly add parentheses around the 2X.
Before this thread I have never heard of implicit operations having higher priority than explicit operations, which honestly sounds like 100% bogus anyway.
You are saying that an implied operation has higher priority than one which I am defining as part of the equation with an operator? Bogus. I don’t buy it. Seriously when was this decided?
I am no mathematics expert, but I have taken up to calc 2 and differential equations and never heard this “rule” before.
deleted by creator
I’m an engineer. Writing by hand I would always use a fraction. If I had to write this in an email or something (quickly and informally) either the context would have to be there for someone to know which one I meant or I would use brackets. I certainly wouldn’t just wrote 1/2x and expect you to know which one I meant with no additional context or brackets
It’s not a law of maths in the way that 1+1=2 is a law
Yes it is, literally! The Distributive Law, and Terms. Also 1+1=2 isn’t a Law, but a definition.
So 1/2x is universally interpreted as 1/(2x)
Correct, Terms - ab=(axb).
people doing academic research in maths, not primary school teachers
Don’t ask either - this is actually taught in Year 7.
if they realise it’s over a question like this they’ll probably end up saying “it’s deliberately ambiguous in an attempt to start arguments”
The university people, who’ve forgotten the rules of Maths, certainly say that, but I doubt Primary School teachers would say that - they teach the first stage of order of operations, without coefficients, then high school teachers teach how to do brackets with coefficients (The Distributive Law).
BDMAS bracket - divide - multiply - add - subtract
I think when a number or variable is adjacent a bracket or parenthesis then it’s distribution to the terms within should always take place before any other multiplication or division outside of it. I think there is a clear right answer and it’s 1.
No there is no clear right answer because it is ambiguous. You would never seen it written that way.
Does it mean A÷[(B)©] or A÷B*C
It’s 16, addition in bracket comes first
Not sure what exactly this convention is called
It’s 2 actual rules of Maths - Terms and The Distributive Law.
never ambiguous
Correct.
there is no right or wrong
Yes there is - obeying the rules is right, disobeying the rules is wrong.
Please Excuse My Dear Aunt Sally, she downloaded a shitty ad-infested calculator from the Google Play store.
[…] the question is ambiguous. There is no right or wrong if there are different conflicting rules. The only ones who claim that there is one rule are the ones which are wrong!
https://people.math.harvard.edu/~knill/pedagogy/ambiguity/index.html
As youngsters, math students are drilled in a particular
convention for the “order of operations,” which dictates the order thus:
parentheses, exponents, multiplication and division (to be treated
on equal footing, with ties broken by working from left to right), and
addition and subtraction (likewise of equal priority, with ties similarly
broken). Strict adherence to this elementary PEMDAS convention, I argued,
leads to only one answer: 16.Nonetheless, many readers (including my editor), equally adherent to what
they regarded as the standard order of operations, strenuously insisted
the right answer was 1. What was going on? After reading through the
many comments on the article, I realized most of these respondents were
using a different (and more sophisticated) convention than the elementary
PEMDAS convention I had described in the article.In this more sophisticated convention, which is often used in
algebra, implicit multiplication is given higher priority than explicit
multiplication or explicit division, in which those operations are written
explicitly with symbols like x * / or ÷. Under this more sophisticated
convention, the implicit multiplication in 2(2 + 2) is given higher
priority than the explicit division in 8÷2(2 + 2). In other words,
2(2+2) should be evaluated first. Doing so yields 8÷2(2 + 2) = 8÷8 = 1.
By the same rule, many commenters argued that the expression 8 ÷ 2(4)
was not synonymous with 8÷2x4, because the parentheses demanded immediate
resolution, thus giving 8÷8 = 1 again.This convention is very reasonable, and I agree that the answer is 1
if we adhere to it. But it is not universally adopted.Everyone in this threading referencing PEMDAS and still thinking the answer is 1 are completely ignoring the part of the convention is left to right. Only way to get 1 is to violate left to right on multiplication and division.
The problem is that BIDMAS and its variants are lies-to-children. Real mathematicians don’t use BIDMAS. Multiplication by juxtaposition is extremely common, and always takes priority over division.
Nobody in their right minds would saw 1/2x is the same as (1/2)x. It’s 1/(2x).
That’s how you get 1. By following conventions used by mathematicians at any level higher than primary school education.
The problem is the /. Usually you’d use a fraction bar, which groups it and makes it unambiguous
There are plenty of contexts where writing in a single flat line is necessary, so it’s still useful to address the issue.
Just using more brackets is always a solution, but it can become messy and hard to read if you take it to the extreme (there’s a Minute Physics video where he does this and it unintentionally shows you just how bad it is), so it eventually becomes a matter of agreeing on convention and using brackets judicially where there’s actual ambiguity.
I only minored in math but I definitely see (1/2)x. That’s how I always entered polynomials into my ti-83 plus
Edit for clarity: I’d enter “1/2x”, as in 0.5x. Casio people have to use parenthesis or explicit multiplication though
Source? I have a hard ass time believing that nobody in their right mind would do pemdas the way you’re supposed to do it xD
The problem is that you’re thinking of BIDMAS as a set of hard rules, rather than the set of rough guidelines created in the early 20th century by one random teacher for the purposes of teaching 10-year-olds how to do the level of maths that 10-year-olds do.
This video and this one point to some examples of style guides in academia as well as practical examples in the published works of mathematicians and physicists, which are pretty consistent.
If you want to come up with a hard rule, doing BIJMDAS, adding in “multiplication indicated by juxtaposition” with the J, is a much better way to do it than what you learnt when you were 10. But even that’s still best to think of as a handy guideline rather than a hard and fast rule.
That’s cool, but still wrong :3
No fr I had no idea that those acronyms weren’t the whole picture, I just assumed some mathematicians a long time ago decided how that stuff should be written out and that BEDMAS/PEMDAS/whatever contained all the rules in it. Thank you for the info, Idk why this isn’t more widely taught, ig because those acronyms are what all the questions are already written for? It doesn’t seem that hard to just teach it as BEADMAS, where the A refers to numbers adjacent to variables
It doesn’t seem that hard to just teach it as BEADMAS, where the A refers to numbers adjacent to variables
Terms already are taught!
Here is an alternative Piped link(s):
Piped is a privacy-respecting open-source alternative frontend to YouTube.
I’m open-source; check me out at GitHub.
Source?
Cajori (1928) for starters, plus any old Year 7 Maths textbook, any era (we know from Lennes letter that textbooks were already doing this in 1917).

That’s cool, but still wrong :3
Exactly, explicit multiplication is part of the parenthesis so it comes first in order of operations
deleted by creator
[…] the question is ambiguous. There is no right or wrong if there are different conflicting rules. The only ones who claim that there is one rule are the ones which are wrong!
https://people.math.harvard.edu/~knill/pedagogy/ambiguity/index.html
Yeah nah. Actual Maths textbooks and proofs - did you not notice the complete lack of references to textbooks in the blog? It’s funny that he mentions Cajori though, given Cajori has a direct reference to Terms #MathsIsNeverAmbiguous

I think I’m gonna trust someone from Harvard over your as-seen-on-TV looking ass account, but thanks for the entertainment you’ve provided by trying to argue with some of the actual mathematicians in here
People keep debating over this stuff. I have a simpler solution. Math is not real.
I’m with the right answer here. / and * have same precedence and if you wanted to treat
2(2+2)as a single unit, you should have written it like(2*(2+2)).this is why I never use ÷ (or more realistically “/”) without explicit brackets denoting order of operations.
Yeah, if there’s any ambiguity, you probably should have written it in a different way.
this comment section illustrates perfectly why i hate maths so much lmao
love ambiguous, confusing rules nobody can even agree on!
The problem isn’t math, it’s the people that suck at at it who write ambigous terms like this, and all the people in the comments who weren’t educated properly on what conventions are.
Yeah, you could easily make this more straightforward by putting parentheses around 8÷2. It’s like saying literature sucks because Finnegans Wake is incomprehensible.
Huge shout out to the jaded AF high school math teachers that don’t give a fuck any more!
lol, math is literally the only subject that has rules set in stone. This example is specifically made to cause confusion. Division has the same priority as multiplication. You go from left to right. problem here is the fact that you see divison in fraction form way more commonly. A fraction could be writen up as (x)/(y) not x/y (assuming x and y are multiple steps). Plain and simple.
The fact that some calculator get it wrong means that the calculator is wrongly configured. The fact that some people argue that you do () first and then do what’s outside it means that said people are dumb.
They managed to get me once too, by everyone spreading missinformation so confidently. Don’t even trust me, look up the facts for yourself. And realise that your comment is just as incorrect as everyone who said the answer is 1. (uhm well they don’t agree on 0^0, but that’s kind of a paradox)
If we had 1/2x, would you interpret that as 0.5x, or 1/(2x)?
Because I can guarantee you almost any mathematician or physicist would assume the latter. But the argument you’re making here is that it should be 0.5x.
It’s called implicit multiplication or “multiplication indicated by juxtaposition”, and it binds more tightly than explicit multiplication or division. The American Mathematical Society and American Physical Society both agree on this.
BIDMAS, or rather the idea that BIDMAS is the be-all end-all of order of operations, is what’s known as a “lie-to-children”. It’s an oversimplification that’s useful at a certain level of understanding, but becomes wrong as you get more advanced. It’s like how your year 5 teacher might have said “you can’t take the square root of a negative number”.
An actual mathematician or physicist would probably ask you to clarify because they don’t typically write division inline like that.
That said, Wolfram-Alpha interprets “1/2x” as 0.5x. But if you want to argue that Wolfram-Alpha’s equation parser is wrong go ahead.
I will happily point out that Wolfram Alpha does this wrong. So do TI calculators, but not Casio or Sharp.
Go to any mathematics professor and give them a problem that includes 1/2x and ask them to solve it. Don’t make it clear that merely asking “how do you parse 1/2x?” is your intent, because in all likelihood they’ll just tell you it’s ambiguous and be done with it. But if it’s written as part of a problem and they don’t notice your true intent, you can guarantee they will take it as 1/(2x).
Famed physicist Richard Feynman uses this convention in his work.
In fact, even around the time that BIDMAS was being standardised, the writing being done doing that standardisation would frequently use juxtaposition at a higher priority than division, without ever actually telling the reader that’s what they were doing. It indicates that at the time, they perhaps thought it so obvious that juxtaposition should be performed first that it didn’t even need to be explained (or didn’t even occur to them that they could explain it).
According to Casio, they do juxtaposition first because that’s what most teachers around the world want. There was a period where their calculators didn’t do juxtaposition first, something they changed to because North American teachers were telling them they should, but the outcry front the rest of the world was enough for them to change it back. And regardless of what teachers are doing, even in America, professors of mathematics are doing juxtaposition first.
I think this problem may ultimately stem from the very strict rote learning approach used by the American education system, where developing a deeper understanding of what’s going on seems to be discouraged in favour of memorising facts like “BIDMAS”.
To be clear, I’m not saying 1/2x being 1/(2x) rather than 0.5x is wrong. But it’s not right either. I’m just pretty firmly in the “inline formulae are ambiguous” camp. Whichever rule you pick, try to apply it consistently, but use some other notation or parenthesis when you want to be clearly understood.
The very fact that this conversation even happens is proof enough that the ambiguity exists. You can be prescriptive about which rules are the correct ones all you like, but that’s not going to stop people from misunderstanding. If your goal is to communicate clearly, then you use a more explicit notation.
Even Wolfram Alpha makes a point of restating your input to show how it’s being interpreted, and renders “1/2x” as something more like
1 - x 2to make very clear what it’s doing.
Even Wolfram Alpha makes a point of restating your input to show how it’s being interpreted
This is definitely the best thing to do. It’s what Casio calculators do, according to those videos I linked.
My main point is that even though there is theoretically an ambiguity there, the way it would be interpreted in the real world, by mathematicians working by hand (when presented in a way that people aren’t specifically on the lookout for a “trick”) would be overwhelmingly in favour of juxtaposition being evaluated before division. Maybe I’m wrong, but the examples given in those videos certainly seem to point towards the idea that people performing maths at a high level don’t even think twice about it.
And while there is a theoretical ambiguity, I think any tool which is operating counter to how actual mathematicians would interpret a problem is doing the wrong thing. Sort of like a dictionary which decides to take an opinionated stance and say “people are using the word wrong, so we won’t include that definition”. Linguists would tell you the job of a dictionary should be to describe how the word is used, not rigidly stick to some theoretical ideal. I think calculators and tools like Wolfram Alpha should do the same with maths.
Linguists would tell you the job of a dictionary should be to describe how the word is used, not rigidly stick to some theoretical ideal. I think calculators and tools like Wolfram Alpha should do the same with maths.
You’re literally arguing that what you consider the ideal should be rigidly adhered to, though.
“How mathematicians do it is correct” is a fine enough sentiment, but conveniently ignores that mathematicians do, in fact, work at WolframAlpha, and many other places that likely do it “wrong”.
The examples in the video showing inline formulae that use implicit priority have two things in common that make their usage unambiguous.
First, they all are either restating, or are derived from, formulae earlier in the page that are notated unambiguously, meaning that in context there is a single correct interpretation of any ambiguity.Second, being a published paper it has to adhere to the style guide of whatever body its published under, and as pointed out in that video, the American Mathematical Society’s style guide specifies implicit priority, making it unambiguous in any of their published works. The author’s preference is irrelevant.
Also, if it’s universally correct and there was no ambiguity in its use among mathematicians, why specify it in the style guide at all?
Here is an alternative Piped link(s):
Famed physicist Richard Feynman uses this convention in his work.
Piped is a privacy-respecting open-source alternative frontend to YouTube.
I’m open-source; check me out at GitHub.
they don’t typically write division inline like that
Yes we do.
But if you want to argue that Wolfram-Alpha’s equation parser is wrong go ahead
Dude, this thread is four months old and I’ve gotten several notifications over the past week from you sporadically responding to comments I barely remember making. Find something better to do with your time than internet argument archeology. I’ll even concede the point if it helps make you go away.
Thanks for the correction, you are right.
Thanks for the correction, you are right
The point is the correction, not who made it. Almost every e-calculator is wrong, so people need to stop trusting them. They’re no more accurate than GPT. Use a proper calculator.
math is literally the only subject that has rules set in stone
go past past high school and this isn’t remotely true
there are areas of study where 1+1=1
…given specific axioms. No rules are being broken.
but which axioms you decide are in use is an arbitrary choice
In modular arithmetic you can make 1+1=0 but I’m struggling to think of a situation where 1+1=1 without redefining the + and = functions.
Not saying you’re wrong, but do you have an example? I’d be interested to see
Off topic, but the rules of math are not set in stone. We didn’t start with ZFC, some people reject the C entirely, then there is intuitionistic logic which I used to laugh at until I learned about proof assistants and type theory. And then there are people who claim we should treat the natural numbers as a finite set, because things we can’t compute don’t matter anyways.
On topic: Parsing notation is not a math problem and if your notation is ambiguous or unclear to your audience try to fix it.
math is literally the only subject that has rules set in stone
Indeed, it does.
This example is specifically made to cause confusion.
No, it isn’t. It simply tests who has remembered all the rules of Maths and who hasn’t.
Division has the same priority as multiplication
And there’s no multiplication here - only brackets and division (and addition within the brackets).
A fraction could be writen up as (x)/(y) not x/y
Neither of those. A fraction could only be written inline as (x/y) - both of the things you wrote are 2 terms, not one. i.e. brackets needed to make them 1 term.
The fact that some people argue that you do () first and then do what’s outside it means that
…they know all the relevant rules of Maths
look up the facts for yourself
You can find them here
your comment is just as incorrect as everyone who said the answer is 1
and 1 is 100% correct.
well they don’t agree on 0^0
Yes they do - it’s 1 (it’s the 5th index law). You might be thinking of 0/0, which depends on the context (you need to look at limits).
are you drunk?
Knowing the rules of Maths means someone might be drunk? Interesting conclusion.
Fuck it, I’m gonna waste time on a troll on the internet who’s necroposting in te hopes that they actually wanna argue the learning way.
This example is specifically made to cause confusion.
No, it isn’t. It simply tests who has remembered all the rules of Maths and who hasn’t.
I said this because of the confusion around the division sign. Almost everyone at some point got it confused, or is just hell bent that one is corrent the other is not. In reality, it is such a common “mistake” that ppl started using it. I’m talking about the classic
4/2x. Ifx = 2, it is:4/2*2 = 2*2 = 44/(2*2) = 4/4 = 1
Wolfram solved this with going with the second if it is an X or another variable as it’s more intuitive.
Division has the same priority as multiplication
And there’s no multiplication here - only brackets and division (and addition within the brackets).
Are you sure ur not a troll? how do you calculate
2(1+1)? It’s4. It’s called implicit multiplication and we do it all the time. It’s the same logic that if a number doesn’t have a sign it’s positive. We could write this up as+2*(+1+(+1)), but it’s harder to read, so we don’t.A fraction could be writen up as (x)/(y) not x/y
Neither of those. A fraction could only be written inline as (x/y) - both of the things you wrote are 2 terms, not one. i.e. brackets needed to make them 1 term.
I don’t even fully understand you here. If we have a faction; at the top we have
1+2and at the bottom we have6-3. inline we could write this as(1+2)/(6-3). The result is 1 as if we simplify it’s3/3.You can’t say it’s
((1+2)/(6-3)). It’s the same thing. You will do the orders differently, but I can’t think of a situation where it’s incorrect, you are just making things harder on yourself.The fact that some people argue that you do () first and then do what’s outside it means that
…they know all the relevant rules of Maths
You fell into the 2nd trap too. If there is a letter or number or anything next to a bracket, it’s multiplication. We just don’t write it out, as why would we, to make it less readable?
2xis the same as2*xand that’s the same as2(x).look up the facts for yourself
You can find them here
I can’t even, you linked social media. The #1 most trust worthy website. Also I can’t even read this shit. This guy talks in hashtags. I won’t waste energy filtering out all the bullshit to know if they are right or wrong. Don’t trust social media. Grab a calculator, look at wolfram docs, ask a professor or teacher. Don’t even trust me!
your comment is just as incorrect as everyone who said the answer is 1
and 1 is 100% correct.
I chose a side. But that side it the more RAW solution imo. let’s walk it thru:
8/2(2+2), let’s remove the confusion8/2*(2+2), brackets8/2*(4), mult & div, left -> right4*(4), let go4*4, the only16, answer
BUT, and as I stated above IF it’d be like:
8/2xwithx=2+2then, we kinda decided to put implicit brackets there so it’s more like8/(2x), but it’s just harder to read, so we don’t.And here is the controversy, we are playing the same game. Because there wasn’t a an explicit multilication, you could argue that it should be handled like the scenario with the x. I disagree, you agree. But even this argument of “like the scenario with the x” is based of what Wolfram decided, there are no rules of this, you do what is more logical in this scenario. It can be a flaw in math, but it never comes up, as you use fractions instead of inline division. And when you are converting to inline, you don’t spear the brackets.
well they don’t agree on 0^0
Yes they do - it’s 1 (it’s the 5th index law). You might be thinking of 0/0, which depends on the context (you need to look at limits).
You said it yourself, if we
lim (x->0) y/xthen there is an answer. But we aren’t in limits.x/0in undefined at all circumstances (I should add that idk abstract algebra & non-linear geometry, idk what happens there. So I might be incorrect here).
And by all means, correct me if I’m wrong. But link something that isn’t an unreadable 3 parted mostodon post like it’s some dumb twitter argument. This is some dumb other platform argument. Or don’t link anything at all, just show me thru, and we know math rules (now a bit better) so it shouldn’t be a problem… as long as we are civilised.
side note: if I did some typos… it’s 2am, sry.
I’m talking about the classic 4/2x. If x = 2, it is:
4/2x2 = 2x2 = 4
4/(2x2) = 4/4 = 1
It’s the latter, as per the definition of Terms. There are references to this definition being used going back more than 100 years.
Wolfram solved this with going with the second if it is an X or another variable as it’s more intuitive
Yes, they do if it’s 2x, but not if it’s 2(2+2) - despite them mathematically being the same thing - leading to wrong answers to expressions such as the OP. In fact, that’s true of every e-calculator I’ve ever seen, except for MathGPT (Desmos used to handle it correctly, but then they made a change to make it easier to enter fractions, and consequently broke evaluating divisions correctly).
how do you calculate 2(1+1)? It’s 4. It’s called implicit multiplication
No, it’s not called implicit multiplication. It’s distribution.
We could write this up as +2*(+1+(+1))
No, you can’t. Adding that multiplication has broken it up into 2 terms. You either need to not add the multiply, or add another set of brackets if you do, to keep it as 1 term.
I can’t think of a situation where it’s incorrect
If a=2 and b=3, then…
1/axb=3/2
1/ab=(1/6)
If there is a letter or number or anything next to a bracket, it’s multiplication
No, it’s distribution. Multiplication refers literally to multiplication signs, of which there aren’t any in this expression.

2x is the same as 2*x
No, 2A is the same as (2xA). i.e. it’s a single Term. 2xA is 2 Terms (multiplied).
If a=2 and b=3, then…
axb=2x3 (2 terms)
ab=6 (1 term)
This guy talks in hashtags.
Only in the first post in each thread, so that people following those hashtags will see the first post, and can then click on it if they want to see the rest of the thread. Also “this guy” is me. :-)
Grab a calculator, look at wolfram docs, ask a professor or teacher
I’m a Maths teacher with a calculator and many textbooks - I’m good. :-) Also, if you’d clicked on the thread you would’ve found textbook references, historical Maths documents, proofs, the works. :-)
8/2(2+2), let’s remove the confusion
8/2*(2+2), brackets
8/2*(4), mult & div, left -> right
4*(4), let go
2 mistakes here. Adding the multiplication sign in the 2nd step has broken up the term in the denominator, thus sending the (2+2) into the numerator, hence the wrong answer (and thus why we have a rule about Terms). Then you did division when there was still unsolved brackets left, thus violating order of operations rules.
it’s more like 8/(2x), but it’s just harder to read, so we don’t
But that’s exactly what we do (but no extra brackets needed around 2x nor 2(2+2) - each is a single term).
you could argue that it should be handled like the scenario with the x
Which is what the rules of Maths tells us to do - treat a single term as a single term. :-)
there are no rules of this
Yeah, there is. :-)
you use fractions instead of inline division
No, never. A fraction is a single term (grouped by a fraction bar) but division is 2 terms (separated by the division operator). Again it’s the definition of Terms.
And by all means, correct me if I’m wrong
Have done, and appreciate the proper conversation (as opposed to those who call me names for simply pointing out the actual rules of Maths).
link something that isn’t an unreadable
No problem. I t doesn’t go into as much detail as the Mastodon thread though, but it’s a shorter read (overall - with the Mastodon thread I can just link to specific parts though, which makes it handier to use for specific points), just covering the main issues.
as long as we are civilised
Thanks, appreciated.
Idk where you teach, but I’m thankful you didn’t teach me.
Let me quizz you, how do you solve
2(2+2)^2? because acording to your linked picture, because brackets are leftmost you do them first. If I were to believe you:(2*2+2*2)^2(4+4)^2, = 64
but it’s just simply incorrect.
2(4)^2, wow we’re at a2x^22*16= 32
The thing that pisses me off most, is the fact that, yes. Terms exists, yes they have all sorts of properties. But they are not rules, they are properties. And they only apply when we have unknows and we’re at the most simplified form. For example your last link, the dude told us that those terms get prio because they are terms!? There are no mention of term prio in the book. It just simply said that when we have a simplified expression like:
2x^2+3x+5we call2x^2and3xand5terms. And yes they get priority, not because we named them those, but because they are multiplications. These help us at functions the most. Where we can assume that the highest power takes the sign at infinity. Maybe if the numbers look right, we can guess where it’d switch sign.I don’t even want to waste energy proofreading this, or telling you the obvious that when we have a div. and a mult. and no x’s there really is no point in using terms, as we just get a single number.
But again, I totally understand why someone would use this, it’s easier. But it’s not the rule still. That’s why at some places this is the default. I forgot the name/keywords but if you read a calculator’s manual there must be a chapter or something regarding this exact issue.
So yeah, use it. It’s good. Especially if you teach physics. But please don’t go around making up rules.
As for your sources, you still linked a blog post.
This is more language/writing style than math. The math is consistent, what’s inconsistent is there are different ways to express math, some of which, quite frankly, are just worse at communicating the mathematical expression clearly than others.
Personally, since doing college math classes, I don’t think I’d ever willingly write an expression like that exactly because it causes confusion. Not the biggest issue for a simple problem, much bigger issue if you’re solving something bigger and need combine a lot of expressions. Just use parentheses and implicit multiplication and division. It’s a lot clearer and easier to work with.
implicit multiplication
Something about the way this thread was written was kind of confusing, so I don’t really get what their point was. Is it just that the terminology is wrong? Or am I missing something?
Like, whatever you call it, a x b, a*b, ab, and a(b) are all acceptable notations to describe the operation “multiply a and b.” Some are nicer to use than others depending on the situation.
Something about the way this thread was written was kind of confusing,
Ok, sorry about that. I’m more than happy to update it if you want to give me some constructive feedback on what was confusing about it. Note though that this was the 3rd part in the series, and maybe you didn’t go back and read the previous 2 parts? They start here
Is it just that the terminology is wrong? Or am I missing something?
Yes and yes. :-) The 2 actual rules of Maths that apply here are Terms and The Distributive Law. These are 2 different rules of Maths - neither of which is “multiplication” - and so when lumping them together as “implicit multiplication” you end up with unpredictable, and usually wrong, answers. The only way to always get the right answer is to follow the actual rules of Maths.
a x b, a*b, ab, and a(b) are all acceptable notations to describe the operation “multiply a and b.”
No, they’re not. The first two are multiplications, the second two are Terms. Note that a Term is a product, the result of a multiplication. In the mnemonics, “Multiplication”" refers literally to multiplication signs, and nothing else.
Ok, sorry about that. I’m more than happy to update it if you want to give me some constructive feedback on what was confusing about it. Note though that this was the 3rd part in the series, and maybe you didn’t go back and read the previous 2 parts? They start here
NP. I’m not really great at giving writing advice, so can’t really help there. Something about it just didn’t click when I read it. The extra context you linked did help a bit.
As far as the issue: After reading it I think it does just seem to be a matter of terminology mixed with problems that arise with when you need to write math expressions inline in text. If you can write things out on paper or use a markdown language, it’s really easy to see how a fractional expression is structured.
8
2(1+3)
is a lot easier to read than 8/2(1+3) even if they technically are meant to be evaluated the same. There’s no room for confusion.
And as for distributive law vs multiplication, maybe this is just taking for granted a thing that I learned a long time ago, but to me they’re just the same thing in practice. When I see a(x+1) I know that in order to multiply these I need to distribute. And if we fill in the algebraic symbols for numbers, you don’t even need to distribute to get the answer since you can just evaluate the parentheses then use the result to multiply by the outside.
Conversely, if I was factoring something, I would need to do division.
ax + a
a
= x+1, thus: a(x+1)
I think we’re basically talking about the same thing, I’m just being a bit lose with the terminology.
And while we’re at it, the best way to make sure there’s no misunderstanding is to just use parenthesis for EVERYTHING! I’m mostly kidding, this can rapidly get unreadable once you nest more than a few parens, although for these toy expressions, it would have the desired effect.
(8)/(2(1+3)) is obviously different than (8/2)(1+3)
It doesn’t have to be confusing. This particular formula is presented in a confusing way. Written differently, the ambiguity is easily resolved.
PEMDAS
Parenthesis, exponents, multiplication, division, addition, subtraction.
The rule is much older than me and they taught it in school. Nothing ambiguous about it, homie. The phone app is fucked up. Calculator nailed it.
Left to right. If you’re following ALL of the rules of PEMDAS then the answer is 16
Multiplication before division bro.
The division goes last.
Answer is 1.
The answer is 1, but the logic you’ve used to get there is a little off. Different groups actually follow different logic, but they usually arrive at the same end-point.
The American Mathematical Society goes:
- Brackets
- Indices
- Multiplication indicated by juxtaposition
- Regular multiplication and division
- Addition and subtraction
While the American Physical Society does
- Brackets
- Indices
- Multiplication
- Division
- Addition and subtraction
In both cases, addition and subtraction are equal in priority (this solves the problem brought up by a different comment where following primary school BIDMAS would mean 8-4+2=2). In one case (and this is the way I prefer to do it) they solve the problem by declaring that implicit multiplication is done before division, but explicit multiplication with the × sign follows the same rules you would have learnt in primary school. The other says all multiplication is done before division, including explicit multiplication.
Multiplication and division have the same priority, whichever one comes first LTR is the one that gets resolved first, so it’s (8 / 2) * 4
By that logic: 8-2+4=2
Of course, it could be kind of ambiguous, but typical convention gives multiplication/division the same priority, as it does addition/subtraction.
And in general, you need to go left to right when dealing with division and subtraction, if other operations have the same priority.
The comment from subignition explains that the phone’s answer, 16, is what you get by strictly following PEMDAS: the rule is that multiplication and division have the same precedence, and you evaluate them from left-to-right.
The calculator uses a different convention where either multiplication has higher priority than division, or where “implicit” multiplication has higher priority (where there is no multiply sign between adjacent expressions).
But explicit multiplication is part of the parenthesis, so still comes before division or exponent
The parentheses step only covers expressions inside parentheses. That’s 2 + 2 in this case. The times-2 part is outside the parentheses so it’s evaluated in a different step.
i know about pemdas and also my brother in christ half the people in the comments are saying the phone app is right lmao
edit: my first answer was 16
Just write it out as a fraction and avoid all the confusion
People in this thread need to watch this: https://youtu.be/lLCDca6dYpA
The calculator is correct
16
spoiler
For anyone like me who has math as their worst subject: PEMDAS.
PEMDAS is an acronym used to mention the order of operations to be followed while solving expressions having multiple operations. PEMDAS stands for P- Parentheses, E- Exponents, M- Multiplication, D- Division, A- Addition, and S- Subtraction.
So we gotta do it in the proper order. And remember, if the number is written like
2(3)then its multiplication, as if it was written2 x 3or2 * 3.So we read
8/2(2+2)and need to do the following;- Read the Parentheses of
(2 + 2)and follow the order of operations within them, which gets us 4. - Then we do
2(4)which is the same as2 x 4which is8 8 / 8is1.
The answer is 1. The old calculator is correct, the phone app which has ads backed into it for a thing that all computers were invented to do is inaccurate.
EDIT: Turns out I’m wrong, but I haven’t been told how or why. I’m willing to learn if people actually tell me, instead of call me wrong and keep it at that. I was told PEMDAS and did PEMDAS.
Well that’s just wrong… Multiplication and division have equal priorities so they are done from left to right. So: 8 / 2 * (2 + 2)=8 / 2 * 4=4 * 4=16
This but unironically
Not quite, pemdas can go either from the left or right (as long as you are consistent) and division is the same priority as multiplication because dividing by something is equal to multiplying by the inverse of that thing… same as subtraction being just addition but you flip the sign.
8×1/2=8/2 1-1=1+(-1)
The result is 16 if you rewrite the problem with this in mind: 8÷2(2+2)=8×(1/2)×(2+2)
I’ve never had anyone tell me operations with the same priority can be done either way, it’s always been left to right.
I’ve always heard it that way too but I think it is for consistency with students, imo Logically, if you are looking at division = multiplying by inverse and subtraction = adding the negative, you should be able to do it both ways. Addition and multiplication are both associative, so we can do 1+2+3 = (1+2)+3 = 1+(2+3) and get the same answer.
But subtraction and division are not associative. Any time you work on paper, 2 - 2 - 2 would equal -2. That is, (2-2)-2=0-2=-2. If you evaluate right to left, you get 2-2-2=2-(2-2)=2-0=2
Correct, subtraction and division are not associative. However, what is subtraction if not adding the opposite of a number? Or division if not multiplying the inverse? And addition and multiplication are associative.
2-2-2 can be written as 2 + (-2) + (-2) which would equal -2 no matter if you solve left to right, or right to left.
In your example with the formula from right to left, distributing the negative sign reveals that the base equation was changed, so it makes sense that you saw a different answer.
2 - (2 - 2) = 2 + ((-2) + 2) = 2
2-(2-2)
But you broke the rule of left-associativity there. You can go right to left provided you keep each number with the sign to it’s left (and you didn’t do that when you separated the first 2 in brackets from it’s minus sign).
I’ve never had anyone tell me operations with the same priority can be done either way, it’s always been left to right
It’s left to right within each operator. You can do multiplication first and division next, or the other way around, as long as you do each operator left to right. Having said that, you also can do the whole group of equal precedence operators left to right - because you’re still preserving left to right for each of the two operators - so you can do multiplication and division left to right at the same time, because they have equal precedence.
Having said that, it’s an actual rule for division, but optional for the rest. The actual rule is you have to preserve left-associativity - i.e. a number is associated with the sign to the left of it - and going left to right is an easy way to do that.
8÷2(2+2)=8×(1/2)×(2+2)
No, that’s wrong. 2(2+2) is a single term, and thus entirely in the denominator. When you separated the coefficient you flipped the (2+2) into the numerator, hence the wrong answer. You must never add multiplication signs where there are none.
Implicit multiplication takes priority over explicit multiplication or division. 2(2+2) is not the same thing as 2*(2+2).
Correct! 2(2+2) is a single term - subject to The Distributive Law - and 2x(2+2) is 2 terms. Those who added a multiply sign there have effectively flipped the (2+2) from being in the denominator to being in the numerator, hence the wrong answer.
But it’s not called “implicit multiplication” - it’s Terms and/or The Distributive Law which applies (and they’re 2 separate rules, so you cannot lump them together as a single rule).
For anyone like me who has math as their worst subject
Admits they suck at math.
Tries to correct the math.
Is wrong.
I’m fuckin’ dead rn 💀
Me searching the place for my old Ti83 after stumbling on this thread.
My partner: why are you even looking for this thing??
Me: Somebody on the Internet is WRONG.
My partner: Good enough, I’ll help!
Removed by mod
I know, it’s good to have someone in your life with priorities.
I happened to have my ti-83 plus next to me. I got 16!
YES finally, some sense in here. 🤣
I ended up downloading a Ti-83 emulator because mine has been devoured by the magical house gremlins.
Except TI calculators also give the wrong answer when a bracketed term has a coefficient.
Then I admit I’m wrong, I just don’t get how PEMDAS/I got it wrong.
Short story, PEMDAS kinda sucks, because it has 4 levels of priority, but 6 letters:
- P
- E
- MD
- AS
M and D are the same level, priority is from left to right.
A and S are the same level, priority is from left to right.Just tested this on a Ti-83 too.
8/2(2+2) = 16

My calculator gets 1. Weird.
My calculator gets 1
That is the correct answer.
I thank you for proving me right, but this a 4 month old thread. Not complaining, just giving you a heads up.
this a 4 month old thread
Yeah, I know, but it’ll show up in search results for all eternity, and it’s full of disinformation. As a Maths teacher/tutor who is sick of hearing “But Google/Wolfram/TI says…”, I’m doing my best to try and get said people to fix their damn calculators (and also make people aware that those calculators are wrong. (sigh) I miss the old days when all calculators gave the right answer - what happened??). If you feel the same way then feel free to share my links - that’s what they’re there for. :-)
And right at the moment I’m feeling too tired to do anything which requires me to think about it, so just doing what I can do on automatic. ;-)
My one big criticism of the Ti-83/84 is implicit multiplication. Ti says 1/2x is 0.5x when I needed the reciprocal of 2x.
Yeah, that’s exactly the problem with TI calculators - ignoring the rules of Maths.
I love you brought the TI truth lul
TI calculators disobey The Distributive Law and give the wrong answer when a bracketed term has a coefficient.
You got it right
Uh… no the 1 is wrong? Division and multiplication have the same precedence, so the correct order is to evaluate from left to right, resulting in 16.
The real correct order is to use brackets to remove ambiguity.
Exactly, these types of problems are designed to make people confused and discuss PEMDAS and drive social media engagement.
There’s no multiplication in this question - multiplication refers literally to multiplication signs - only division and brackets, and addition within the brackets. So you have to use The Distributive Law to solve the brackets, then do the division, giving you 1.
The problem with this is that the division symbol is not an accurate representation of the intended meaning. Division is usually written in fractions which has an implied set of parenthesis, and is the same priority as multiplication. This is because dividing by a number is the same as multiplying by the inverse, same as subtracting is adding the negative of a number.
8/2(2+2) could be rewritten as 8×1/2×(2+2) or (8×(2+2))/2 which both resolve into 16.
You left out the way it can be rewritten which most mathematicians would actually use, which is 8/(2(2+2)), which resolves to 1.
not to be That Guy, but the phone is actually correct… multiplication and division have the same precedence, so
8 / 2 * 4should give the same result as8 * 4 / 2, ie 16but the phone is actually correct
No, it’s actually wrong.
8 / 2 * 4
It’s 8/(2x4). You can’t remove brackets unless there is only 1 term left inside.
P E M D A S
vs
P E M/D A/S
The latter is correct, Multiplication/Division, and Addition/Subtraction each evaluate left to right (when not made unambiguous by Parentheses). I.e., 6÷2×3 = 9, not 1. That said, writing the expression in a way that leaves ambiguity is bad practice. Always use parentheses to group operations when ambiguity might arise.
Ignore the idiots telling you you’re wrong. Everyone with a degree in math, science or engineering makes a distinction between implicit and explicit multiplication and gives implicit multiplication priority.
You are correct. This is the right sequence of operations done here.
PEMDAS evaluated from left to right. If you followed that you’d get 16. 1 is ignoring left to right.
The problem is that the way PEMDAS is usually taught multiplication and division are supposed to have equal precedence. The acronym makes it look like multiplication comes before division, but you’re supposed to read MD and as one step. (The same goes for addition and subtraction so AS is also supposed to be one step.) It this example the division is left of the multiplication so because they have equal precedence (according to PEMDAS) the division applies first.
IMO it’s bad acronym design. It would be easier if multiplication did come before division because that is how everyone intuitively reads the acronym.
Maybe it should be PE(M/D)(A/S). But that version is tricky to pronounce. Or maybe there shouldn’t be an acronym at all.
You’re a lifesaver, thank you so much. I actually didn’t know about PEMDAS, I was never taught it before…
They’re actually wrong though.
There’s 4 levels to PEMDAS, not 6.
- Parenthese
- Exponent
- Multiplication or Division
- Addition or Substraction
Also,
https://www.symbolab.com/solver/step-by-step/8\div2(2%2B2)?or=input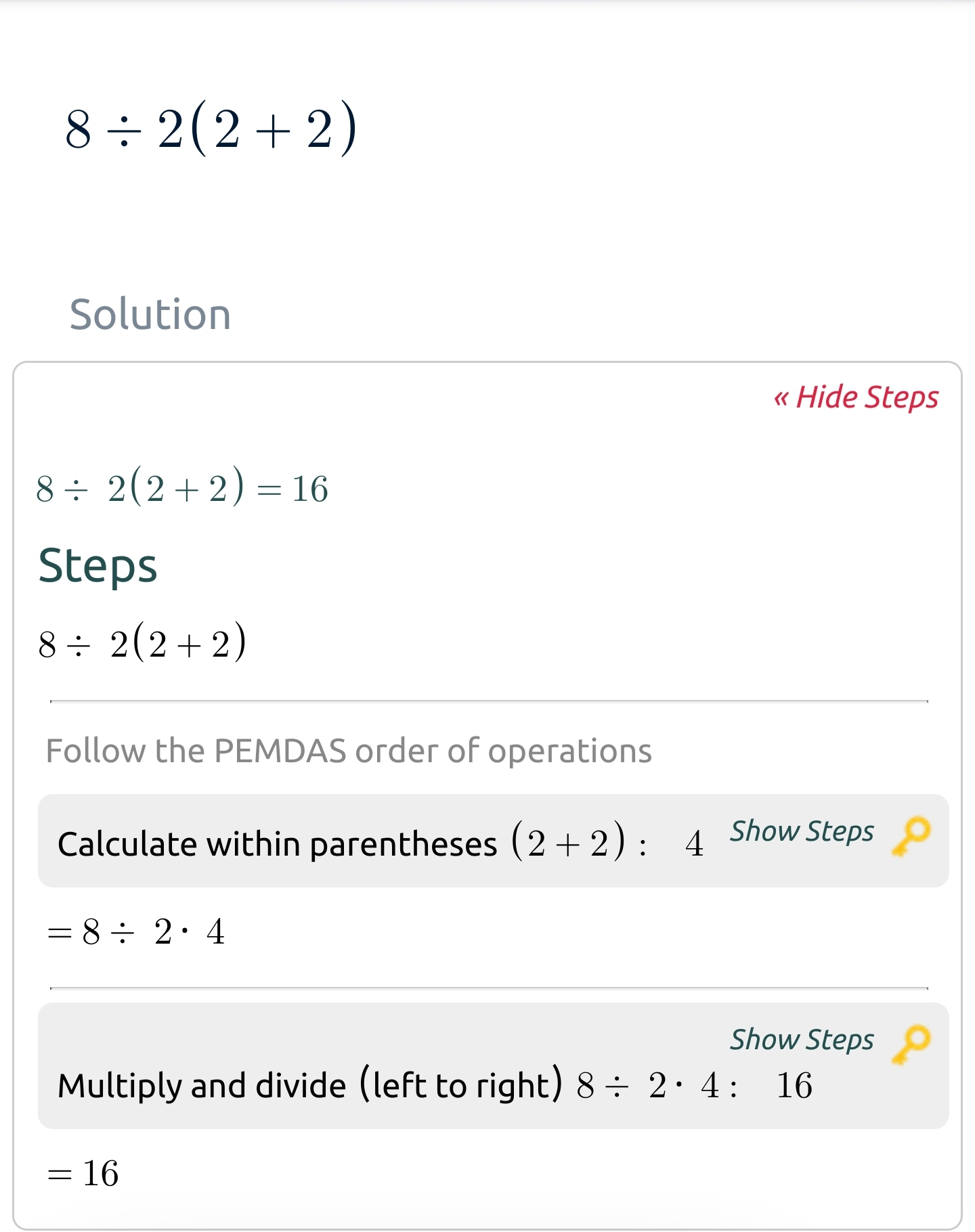
Like @LopensLeftArm@sh.itjust.works mentioned:
PEMDAS should be read as Parentheses, Exponents, Multiplication and Division, Addition and Subtraction. There are four levels of priority, not six.
Ohh, I see. Thank you for clarifying, Math has always been the bane of my existence. x_x
- Read the Parentheses of
































